Sometimes scientists and engineers have the misfortune of being born too early. Not just a decade or two early, but generations. Charles Babbage is one. Lewis Fry Richardson
(1881-1953) is another.
Lewis Fry Richardson was born to a Quaker family and was a life-long pacifist. His parents, who owned a leather goods factory, were well off, and saw to it that he got a first rate education. In 1898 he attended the Durham College of Science, where he took courses in mathematical physics, chemistry, botany, and zoology, excelling in them all. He was interested in many sciences and remained so for the rest of his life. In 1900 he received a scholarship to Kings College, Cambridge, where he took the Natural Sciences Tripos, a course of study for people interested in many sciences. He graduated first in his class. His refusal to specialize prevented him from receiving a doctorate at that time, although ultimately he did receive a doctorate in mathematical psychology from the University of London in 1928.
In 1909 he married Dorothy Gannet, to whom he stayed married for the rest of his life. They were happy together, but also had sadness. They experienced 3 miscarriages, despite both being healthy. Only much later did they realize they had incompatible blood types---he was RH positive and she was RH negative. They adopted two sons and a daughter between 1920 and 1927.
Richardson's career reflects his eclectic interests:
* National Physical Laboratory (1903–1904)
* University College Aberystwyth (1905–1906)
* chemist, National Peat Industries (1906–1907)
* National Physical Laboratory (1907–1909)
* manager of the physical and chemical laboratory, Sunbeam Lamp Company (1909–1912)
* Manchester College of Technology (1912–1913)
* Meteorological Office - as superintendent of Eskdalemuir Observatory (1913–1916)
* Friends Ambulance Unit in France (1916–1919)
* Meteorological Office at Benson, Oxfordshire (1919–1920)
* Head of the Physics Department at Westminster Training College (1920–1929)
* Principal, Paisley Technical College, now part of the University of the West of Scotland (1929–1940)
In 1926, he was elected to the Fellowship of the Royal Society
Richardson made original contributions in many fields, but today is known chiefly for his meteorological insights and his research into fractals (a branch of mathematics not named for more than 20 years after he died.
A brief description of his work in fractals is worthy of mention.
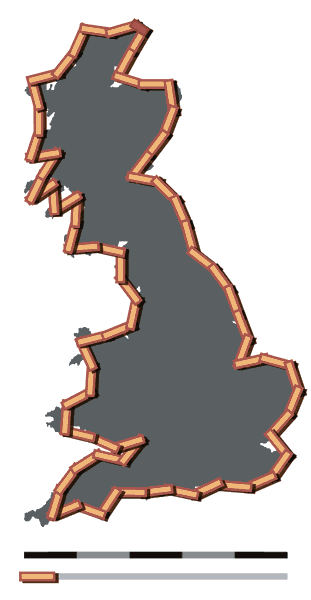
A lifelong pacifist (he did not fight in World War I, and was an ambulance driver) he wondered if there was a mathematical basis for countries going to war with each other. In his research, he came across widely varying figures for the length of borders between nations. For instance, 380 km or 449 km between The Netherlands and Belgium. 987 km or 1,214 km between Spain and Portugal. How could this be?
He dropped his research into the mathematical causes of war between countries for a while, and wondered about the coastline of Britain.
He measured the coastline of Britain using a 200 km ruler:
Then with a 100 km ruler:
Then with a 50 km ruler:
Notice how the length of the coastline increases every time one uses a finer unit to measure! Richardson proved that there was no final measurement of the length of the coastline that could be made. For an irregular object, measuring its perimeter depends on the length of the unit you are using to make the measurement. The smaller the unit of measurement, the greater the total perimeter will be. This work was ignored for more than 40 years, but when Benoit Mandelbrot ran across it in the 1960s, it became the inspiration for his work How Long is the Coastline of Britain (1967), which was the beginning of his development of fractal geometry.
Richardson also made original contributions to numerical analysis, developing new equations for the convergence of a sequence. Details of his mathematical work in this field are here.
Richardson also created a new iterative method for solving linear equations, which is now known as the Richardson Iteration Method
Richardson's mathematical contributions to meteorology began with his investigations into the mathematics of turbulence. He developed a way of calculating the ratio of potential energy to kinetic energy:
in which g is the acceleration due to gravity, h a representative vertical lengthscale, and u a representative speed.
When considering flows in which density differences are small it is common to use the reduced gravity g' and the relevant parameter is the densimetric Richardson number.
Richardson was always interested in meteorology, and through his work as an javascript:void(0)ambulance driver in World War I, he made the first computational weather forecast. He collected observation records over central Europe for an arbitrary day he chose, May 20, 1910, with measurements of atmospheric characteristics and vectors according to the new Bjerknes paradigm and tried to calculate what the weather would be in 3 days time. It was very difficult and intricate computational work, and he had to deal with interruptions not typical for today's research scientists. In April 1917 when the German army was on a local offensive, his ambulance was shelled and he had to get out of the wreckage and bury his notebooks in a metal container in a local churchyard. Then the German army took over and he had to wait for months to go back when the village was retaken. Fortunately his work survived.
His computations were discouraging. His first 'retrocast' showed impossible barometric pressure rises of more than 4.3 inches (135 mb) over central Europe, and he was discouraged. He also had a good mathematical intuition---that small variances in initial conditions would have big impacts on the future weather---a step towards chaos theory (which came from Edward Norton Lorenz in the 1960s and 1970s, also a meteorologist)
Richarson composed a little poem:
Big whirls have little whirls
That feed on their velocity
And little whirls have lesser whirls
And so on to viscosity
The error was not identified until 2007. The error had to do with a smoothing method for interpolating between data points--Richardson had known about this method, but being shell-shocked had just forgot! Without the error, his forecast was basically correct. Three days out.
But he never knew that.
Richardson conceived of a way to forecast weather accurately, worldwide, in advance. He imagined 60,000 mathematicians working at any one time on the weather, 300,000 in shifts. With data from aircraft, a worldwide network of balloons, station observations, ships, buoys, all transmitted to computers to work out the data.
But not computers the way we think of them. Computers were the people doing the computing! And I have to imagine it would be tedious work! It's like something out of a John Varley novella. At this moment Overdrawn at the Memory Bank is replaying in my head ;)
Richardson wrote all this out in a monumental work that reads as much like science fiction as science, Weather Prediction by Numerical Processes (1922). It is well worth a read in the original.
Here is a passage from the book:
“After so much hard reasoning, may one play with a fantasy? Imagine a large hall like a theatre, except that the circles and galleries go right round through the space usually occupied by the stage. The walls of this chamber are painted to form a map of the globe. The ceiling represents the north polar regions, England is in the gallery, the tropics in the upper circle, Australia on the dress circle and the Antarctic in the pit.
A myriad computers are at work upon the weather of the part of the map where each sits, but each computer attends only to one equation or part of an equation. The work of each region is coordinated by an official of higher rank. Numerous little "night signs" display the instantaneous values so that neighbouring computers can read them. Each number is thus displayed in three adjacent zones so as to maintain communication to the North and South on the map.
From the floor of the pit a tall pillar rises to half the height of the hall. It carries a large pulpit on its top. In this sits the man in charge of the whole theatre; he is surrounded by several assistants and messengers. One of his duties is to maintain a uniform speed of progress in all parts of the globe. In this respect he is like the conductor of an orchestra in which the instruments are slide-rules and calculating machines. But instead of waving a baton he turns a beam of rosy light upon any region that is running ahead of the rest, and a beam of blue light upon those who are behindhand.
Four senior clerks in the central pulpit are collecting the future weather as fast as it is being computed, and despatching it by pneumatic carrier to a quiet room. There it will be coded and telephoned to the radio transmitting station. Messengers carry piles of used computing forms down to a storehouse in the cellar.
In a neighbouring building there is a research department, where they invent improvements. But these is much experimenting on a small scale before any change is made in the complex routine of the computing theatre. In a basement an enthusiast is observing eddies in the liquid lining of a huge spinning bowl, but so far the arithmetic proves the better way. In another building are all the usual financial, correspondence and administrative offices. Outside are playing fields, houses, mountains and lakes, for it was thought that those who compute the weather should breathe of it freely.”
Richardson of course knew that the idea of 300,000 mathematicians employed for computing the weather was a fantasy. But it would work!
Richardson thought he would never live to see it: "Perhaps some day in the dim future it will be possible to advance the computations faster than the weather
advances.....But that is a dream."
Richardson discussed the way the meteorologists of his time made forecasts---they studied the maps they created, remembered past occasions when the maps were similar, and made forecasts based on what happened next during prior occasions when the weather maps were similar. Richardson took a dim view of this.
"The forecast is based on the supposition that what the atmosphere
did then, it will do again now.....The past history of the atmosphere is used, so to speak, as a full-scale working model of its present self"
Richardson compared this to astronomical predictions of the positions of the planets and stars:
"The Nautical Almanac, that marvel of accurate forecasting, is not based on the principle that astronomical history repeats itself in the aggregate. It would be safe to say that a particular disposition of stars, planets and satellites never occurs twice. Why then should we expect a present weather map to be exactly represented in a catalogue of past weather?"
Another quote from Richardson:
"The scheme is complicated because the atmosphere is complicated."
The 'scheme' referring to hundreds of thousands of mathematicians working on the weather.
Inexplicably, wikipedia does not have an article on "Weather Prediction by Numerical Process". Fortunately, google books does have it. Credit to John for finding it when I failed!
Reviews of "Weather Prediction by Numerical Process" were quite positive, although many thought the idea of using computational power--either through hundreds of thousands of mathematicians or by mechanical calculators to be a fantasy. There was also the problem of his forecast for May 20, 1910--with the wildly high barometric pressure. The book didn't sell well, and dropped out of sight. I came across it on the stacks of the GA Tech library in 1993 and read it---it was fascinating to me.
Richardson left the Meteorological Office in 1920 when it was made a part of the Air Ministry, which later became part of the Ministry of Defence. As "Weather Prediction by Numerical Process" was being published, Richardson discovered that his work on meteorology and atmospheric motion was being used to predict how to deploy mustard gas and chlorine--gas warfare. Richardson, as a life-long pacifist, was outraged. He removed all his work and notes from his office, destroyed them and then resigned. That caused a lot of controversy, but it did not stop him from being elected as a fellow of the Royal Society in 1926.
Disillusioned with the military appropriation of his work for gas warfare, he became interested in psychology (recall his doctorate) and the mathematics of violence. He worked in that field for the rest of his life, although maintaining himself in other disciplines. In 1949 Richardson published "Arms and Insecurity" in which he demonstrated that the length of two countries' common border was very strongly correlated with the risk of their going to war, among other factors. In 1950, he published "Statistics of Deadly Quarrels" in which he researched every conflict from 1815 to 1945 and discovered that the size of wars' death tolls varied by a logrithmic scale, very close to a base ten logarithmic scale. There were many more small conflicts than large ones, and the death tolls followed a Poisson distribution very closely. Richardson also determined this was true for gangland murders in Chicago and Shanghai---there were very many cases of one or two murders, 3 or 4 being less common and incidents like the St. Valentine's Day Massacre being very rare.
Richardson was not quite as out of time as Charles Babbage. Babbage never saw a modern computer. But Richardson was still alive when ENIAC made the first weather prediction in 1950. Richardson called it "an enormous advance".
A truly excellent summation of the history of numerical weather prediction is The origins of computer weather prediction and climate modeling by Peter Lynch. It is well worth a read!



No comments:
Post a Comment